Cours de quatrième

6 - Les fonctions

Comme nous l'avons vu en cinquième, une fonction est une sorte de machine à laquelle on donne des nombres et qui en retourne d'autres. Les fonctions sont utiles pour l'étude et la représentation de tous les phénomènes qui évoluent et sont omniprésentes dans toutes les sciences.

Nous avons déjà vu comment écrire une fonction et comment calculer l'image d'un nombre par une fonction. Dans ce nouveau cours, nous allons voir comment représenter graphiquement une fonction et ce qu'est un antécédent d'un nombre par une fonction.

Représentation graphique d'une fonction

La représentation graphique d'une fonction est une courbe qui permet de visualiser comment la fonction agit sur les nombres.

Méthode

Pour tracer la représentation graphique d'une fonction :

1. On dessine deux axes gradués perpendiculaires.
2. On choisit des valeurs de x comme on veut et on calcule les images f(x) correspondantes.
3. Pour chaque x choisi, on se positionne en x sur l'axe horizontal des abscisses 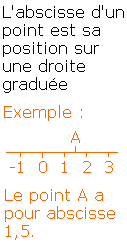et on place un point ou une croix à la hauteur f(x).
4. On relie les points obtenus de manière harmonieuse.

Exemple

Représentation graphique de la fonction .

1.
2. Prenons les x de -2 à 2. On a f(-2)=4, f(-1)=1, f(0)=0, f(1)=1 et f(2)=4.
3.
4.

As-tu compris ?

Antécédent d'un nombre par une fonction

Parfois, nous connaissons une fonction et nous avons besoin de trouver le ou les nombre(s) qui ont pour image un nombre donné.
C'est un peu un texte à trous.

Exemple
On doit trouver le nombre x pour lequel la fonction est égale à 67.
Nous devrons donc trouver le nombre ? tel que 2×?+7=67.

Ce nombre s'appelle un antécédent de 67 par f.

Définition

Un antécédent d'un nombre b par une fonction f est un nombre a tel que f(a)=b.

Remarques

Un nombre N possède toujours une seule image par une fonction, mais peut posséder plusieurs antécédents.
Par exemple, le nombre 9 possède deux antécédents par . Ce sont 3 et -3.

Un nombre peut aussi ne pas posséder d'antécédent.
Pour cette même fonction , le nombre -16 ne possède pas d'antécédent.

As-tu compris ?

>>> Le théorème de Pythagore >>>

Les fonctions en quatrième

cours, vidéos, exercices, questions (0)