Cours de seconde
3 - Les fonctions
Nous avons déjà vu les fonctions au collège : en cinquième, nous avons vu des notations et le calcul d'images , en quatrième la représentation graphique d'une fonction et la notion d'antécédent
, en quatrième la représentation graphique d'une fonction et la notion d'antécédent d'un nombre par une fonction.
En troisième, nous avons vu le calcul et la lecture des antécédents ainsi que les fonctions affines et linéaires
d'un nombre par une fonction.
En troisième, nous avons vu le calcul et la lecture des antécédents ainsi que les fonctions affines et linéaires .
.
Dans ce cours, nous allons voir ce qu'est l'ensemble de définition d'une fonction, son tableau de variation
d'une fonction, son tableau de variation , comment faire un tableau de variation et nous allons étudier deux fonctions particulières :
fonction carré
, comment faire un tableau de variation et nous allons étudier deux fonctions particulières :
fonction carré et fonction inverse
et fonction inverse .
.
Les fonctions sont omniprésentes dans toutes les sciences, car elles décrivent comment des variables se comportent par rapport à d'autres.
Par exemple, une population d'animaux en fonction de la population de leurs prédateurs, la luminosité d'une étoile en fonction de sa distance et de son âge, l'aire d'une figure en fonction de la longueur d'un côté, etc.
L'étude des fonctions permet de faire des prévisions et des optimisations dans le cas de problèmes particuliers en sciences et en économie.
Ensemble de définition
L'ensemble de définition d'une fonction est l'ensemble des valeurs de x pour lesquelles on peut calculer f(x).
Exemples
L'ensemble de définition de la fonction ![]() est
est ![]() .
.
L'ensemble de définition de la fonction ![]() est
est ![]() .
.
L'ensemble de définition de la fonction ![]() est
est ![]() . (pourquoi)
. (pourquoi)
Comment déterminer l'ensemble de définition
Pour déterminer l'ensemble de définition d'une fonction :
1. Si la fonction contient une racine carrée
Si la fonction contient une racine carrée , alors il faut que l'expression sous la racine soit positive pour qu'on puisse calculer les images.
, alors il faut que l'expression sous la racine soit positive pour qu'on puisse calculer les images.
Pour ![]() , on commence par résoudre l'inéquation
, on commence par résoudre l'inéquation g(x)≥0.
g(x)≥0.
L'ensemble de définition est l'ensemble des solutions de cette inéquation.
2. Si la fonction contient un quotient
Si la fonction contient un quotient , alors il faut que le dénominateur
, alors il faut que le dénominateur soit différent de zéro pour qu'on puisse calculer les images.
soit différent de zéro pour qu'on puisse calculer les images.
Pour ![]() , on commence par résoudre l'équation
, on commence par résoudre l'équation h(x)=0.
h(x)=0.
L'ensemble de définition est l'ensemble des nombres réels moins les éventuelles solutions de cette équation.
3. Autres cas
Pour toutes les autres fonctions vues en seconde, s'il n'y a pas de racine carrée ni de quotient, l'ensemble de définition est ![]() .
.
Exemples
1. Pour ![]() , on résout l'inéquation
, on résout l'inéquation 14-7x≥0.
14-7x≥0.
On trouve x≤2 donc D=]-∞;2].
2. Pour ![]() , on résout l'équation
, on résout l'équation 2x-8=0.
2x-8=0.
On trouve x=4, donc D=]-∞,4[U]4;+∞[.
Entraînement
Variation de fonction
Voyons maintenant ce que sont les fonctions croissantes et décroissantes.
Fonction croissante
Si, sur un intervalle de l'axe des abscisses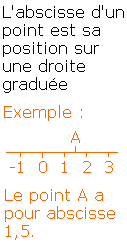 , la courbe d'une fonction monte, alors on dit que cette fonction est croissante sur cet intervalle.
, la courbe d'une fonction monte, alors on dit que cette fonction est croissante sur cet intervalle.
Une fonction croissante est une fonction qui conserve l'ordre des images : si a et b sont deux nombres tels que a<b, alors f(a)<f(b).

Fonction décroissante
Si, sur un intervalle de l'axe des abscisses, la courbe d'une fonction descend, alors on dit que la fonction est décroissante sur cet intervalle.
Une fonction décroissante est une fonction qui change l'ordre des images : si a et b sont deux nombres tels que a<b, alors f(a)>f(b).

Petite question
Tableau de variation
Pour représenter et visualiser les variations d'une fonction, on utilise un tableau de variation.
Un tableau de variation est un tableau composé de deux lignes et de plusieurs colonnes :
La première ligne contient les valeurs de l'ensemble de définition et les valeurs pour lesquelles les variations changent.
La deuxième ligne contient des flèches qui indiquent le sens de variation de la fonction pour les valeurs de x correspondantes sur la première ligne.
Comment faire un tableau de variation ?
- 1. On écrit sur la première ligne les valeurs de x pour lesquelles le sens de variation change.
- 2. En dessous, on symbolise par des flèches les variations de f.
- 3. Aux extrémités des flèches, on écrit les valeurs prises par la fonction.

Fonction carré, fonction inverse
Fonction carré
La fonction f:x↦x² s'appelle la fonction carré.
Nous avons tracé ci-dessus son tableau de variation.
Sa courbe est une parabole.

Fonction inverse
La fonction ![]() est la fonction inverse.
est la fonction inverse.
Sa courbe est une hyperbole.

Les fonctions en seconde sur cmath.fr
cours, cours en vidéo, exercices, questions (2)
Sur le même thème
• Cours de cinquième sur les fonctions. Vocabulaire, notations, image d'un nombre par une fonction.
• Cours de quatrième sur les fonctions. Représentation graphique, notion d'antécédent.
• Cours de troisième sur les fonctions. Calcul et lecture d'antécédent, les fonctions affines.
• Cours de première sur la dérivation. Nombre dérivé et dérivation, fonction dérivée, formules et règles de dérivation.
• Cours de première sur l'étude de fonction. Etude des variations d'une fonction, fonctions usuelles.
• Cours de première sur les fonctions. La fonction exponontielle et les fonctions trigonométriques.
• Cours de terminale sur les fonctions. Fonctions exponentielle et logarithme népérien, dérivée d'une fonction composée et théorème des valeurs intermédiaires.
Sponsorisé
• Cours de maths. Trouvez un professeur en ligne ou près de chez vous en Belgique avec Superprof.